# setwd("Your work directory")
options(stringsAsFactors = FALSE)
library(tm)
require(topicmodels)

textdata <- read.csv("data/sotu.csv", sep = ";", encoding = "UTF-8")
english_stopwords <- readLines("resources/stopwords_en.txt", encoding = "UTF-8")

# Create corpus object
m <- list(ID = "id", content = "text", DateTimeStamp = "date")
myReader <- readTabular(mapping = m)
corpus <- Corpus(DataframeSource(textdata), readerControl = list(reader = myReader))

# Preprocessing chain
processedCorpus <- tm_map(corpus, removePunctuation, preserve_intra_word_dashes = TRUE)
processedCorpus <- tm_map(processedCorpus, removeNumbers)
processedCorpus <- tm_map(processedCorpus, content_transformer(tolower))
processedCorpus <- tm_map(processedCorpus, removeWords, english_stopwords)
processedCorpus <- tm_map(processedCorpus, stemDocument, language = "en")
processedCorpus <- tm_map(processedCorpus, stripWhitespace)

1 Model calculation

After the preprocessing, we have two corpus objects: processedCorpus, on which we calculate an LDA topic model [1]. To this end, stopwords were removed, words were stemmed and converted to lowercase letters and special characters were removed. The second Corpus object corpus serves to be able to view the original texts and thus to facilitate a qualitative control of the topic model results.

We now calculate a topic model on the processedCorpus. For this purpose, a DTM of the corpus is created. In this case, we only want to consider terms that occur with a certain minimum frequency in the body. This is primarily used to speed up the model calculation.

# compute document term matrix with terms >= minimumFrequency
minimumFrequency <- 5
DTM <- DocumentTermMatrix(processedCorpus, control = list(bounds = list(global = c(minimumFrequency, Inf))))

# have a look at the number of documents and terms in the matrix
dim(DTM)

## [1]  231 7673

As an unsupervised machine learning method, topic models are suitable for the exploration of data. The calculation of topic models aims to determine the proportionate composition of a fixed number of topics in the documents of a collection. It is useful to experiment with different parameters in order to find the most suitable parameters for your own analysis needs.

For parameterized models such as Latent Dirichlet Allocation (LDA), the number of topics K is the most important parameter to define in advance. How an optimal K should be selected depends on various factors. If K is too small, the collection is divided into a few very general semantic contexts. If K is too large, the collection is divided into too many topics of which some may overlap and others are hardly interpretable.

For our first analysis we choose a thematic “resolution” of K = 20 topics. In contrast to a resolution of 100 or more, this number of topics can be evaluated qualitatively very easy.

# load package topicmodels
require(topicmodels)
# number of topics
K <- 20
# set random number generator seed
set.seed(9161)
# compute the LDA model, inference via 1000 iterations of Gibbs sampling
topicModel <- LDA(DTM, K, method="Gibbs", control=list(iter = 500, verbose = 25))

Depending on the size of the vocabulary, the collection size and the number K, the inference of topic models can take a very long time. This calculation may take several minutes. If it takes too long, reduce the vocabulary in the DTM by increasing the minimum frequency in the previous step.

The topic model inference results in two (approximate) aposteriori probability distributions: a distribution theta over K topics within each document and a distribution beta over V terms within each topic, where V represents the length of the vocabulary of the collection (V = 7673). Let’s take a closer look at these results:

# have a look a some of the results (posterior distributions)
tmResult <- posterior(topicModel)
# format of the resulting object
attributes(tmResult)

## $names
## [1] "terms"  "topics"

nTerms(DTM)              # lengthOfVocab

## [1] 7673

# topics are probability distribtions over the entire vocabulary
beta <- tmResult$terms   # get beta from results
dim(beta)                # K distributions over nTerms(DTM) terms

## [1]   20 7673

rowSums(beta)            # rows in beta sum to 1

##  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 
##  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1

nDocs(DTM)               # size of collection

## [1] 231

# for every document we have a probaility distribution of its contained topics
theta <- tmResult$topics 
dim(theta)               # nDocs(DTM) distributions over K topics

## [1] 231  20

rowSums(theta)[1:10]     # rows in theta sum to 1

##  1  2  3  4  5  6  7  8  9 10 
##  1  1  1  1  1  1  1  1  1  1

Let’s take a look at the 10 most likely terms within the term probabilities beta of the inferred topics (only the first 8 are shown below).

terms(topicModel, 10)

##       Topic 1    Topic 2    Topic 3   Topic 4     Topic 5    Topic 6    
##  [1,] "war"      "govern"   "nation"  "program"   "world"    "america"  
##  [2,] "men"      "duti"     "war"     "year"      "nation"   "american" 
##  [3,] "american" "peopl"    "part"    "nation"    "free"     "freedom"  
##  [4,] "forc"     "time"     "peac"    "increas"   "freedom"  "nation"   
##  [5,] "enemi"    "regard"   "forc"    "feder"     "peopl"    "secur"    
##  [6,] "fight"    "hope"     "author"  "congress"  "defens"   "countri"  
##  [7,] "unit"     "part"     "million" "state"     "strength" "world"    
##  [8,] "peac"     "justic"   "unit"    "develop"   "econom"   "terrorist"
##  [9,] "product"  "question" "debt"    "continu"   "militari" "peopl"    
## [10,] "part"     "make"     "commerc" "administr" "effort"   "terror"   
##       Topic 7     Topic 8   
##  [1,] "state"     "state"   
##  [2,] "constitut" "unit"    
##  [3,] "union"     "congress"
##  [4,] "power"     "govern"  
##  [5,] "peopl"     "great"   
##  [6,] "congress"  "year"    
##  [7,] "territori" "act"     
##  [8,] "presid"    "treati"  
##  [9,] "law"       "power"   
## [10,] "republ"    "duti"

For the next steps, we want to give the topics more descriptive names than just numbers. Therefore, we simply concat the five most likely terms of each topic to a string that represents a pseudo-name for each topic.

top5termsPerTopic <- terms(topicModel, 5)
topicNames <- apply(top5termsPerTopic, 2, paste, collapse=" ")

2 Visualization of Words and Topics

Although wordclouds may not be optimal for scientific purposes they can provide a quick visual overview of a set of terms. Let’s look at some topics as wordcloud.

In the following code, you can change the variable topicToViz with values between 1 and 20 to display other topics.

require(wordcloud)
# visualize topics as word cloud
topicToViz <- 11 # change for your own topic of interest
topicToViz <- grep('mexico', topicNames)[1] # Or select a topic by a term contained in its name
# select to 40 most probable terms from the topic by sorting the term-topic-probability vector in decreasing order
top40terms <- sort(tmResult$terms[topicToViz,], decreasing=TRUE)[1:40]
words <- names(top40terms)
# extract the probabilites of each of the 40 terms
probabilities <- sort(tmResult$terms[topicToViz,], decreasing=TRUE)[1:40]
# visualize the terms as wordcloud
mycolors <- brewer.pal(8, "Dark2")
wordcloud(words, probabilities, random.order = FALSE, color = mycolors)

Let us now look more closely at the distribution of topics within individual documents. To this end, we visualize the distribution in 3 sample documents.

Let us first take a look at the contents of three sample documents:

exampleIds <- c(1, 100, 200)
lapply(corpus[exampleIds], as.character)

## [1] "1: Fellow-Citizens of the Senate and House of Representatives:\n\nI embrace with great satisfaction the opportunity which now presents itself\nof congratulating you on the present favorable prospects of our public\naffairs. The recent accession of the important state of North Carolina to\nthe Constitution of the United States (of which official information has\nbeen received), the rising credit and respect..."

## [1] "100: To the Congress of the United States:\n\nAs you assemble for the discharge of the duties you have assumed as the\nrepresentatives of a free and generous people, your meeting is marked by an\ninteresting and impressive incident. With the expiration of the present\nsession of the Congress the first century of our constitutional existence\nas a nation will be completed.\n\nOur survival for one hundred years ..."

## [1] "200: Mr. Speaker, Mr. President, distinguished Members of Congress, honored\nguests, and fellow citizens:\n\nMay I congratulate all of you who are Members of this historic 100th\nCongress of the United States of America. In this 200th anniversary year of\nour Constitution, you and I stand on the shoulders of giants--men whose\nwords and deeds put wind in the sails of freedom. However, we must always\nremember..."

After looking into the documents, we visualize the topic distributions within the documents.

# load libraries for visualization
library("reshape2")
library("ggplot2")
N <- length(exampleIds)
# get topic proportions form example documents
topicProportionExamples <- theta[exampleIds,]
colnames(topicProportionExamples) <- topicNames
vizDataFrame <- melt(cbind(data.frame(topicProportionExamples), document = factor(1:N)), variable.name = "topic", id.vars = "document")  

ggplot(data = vizDataFrame, aes(topic, value, fill = document), ylab = "proportion") + 
  geom_bar(stat="identity") +
  theme(axis.text.x = element_text(angle = 90, hjust = 1)) +  
  coord_flip() +
  facet_wrap(~ document, ncol = N)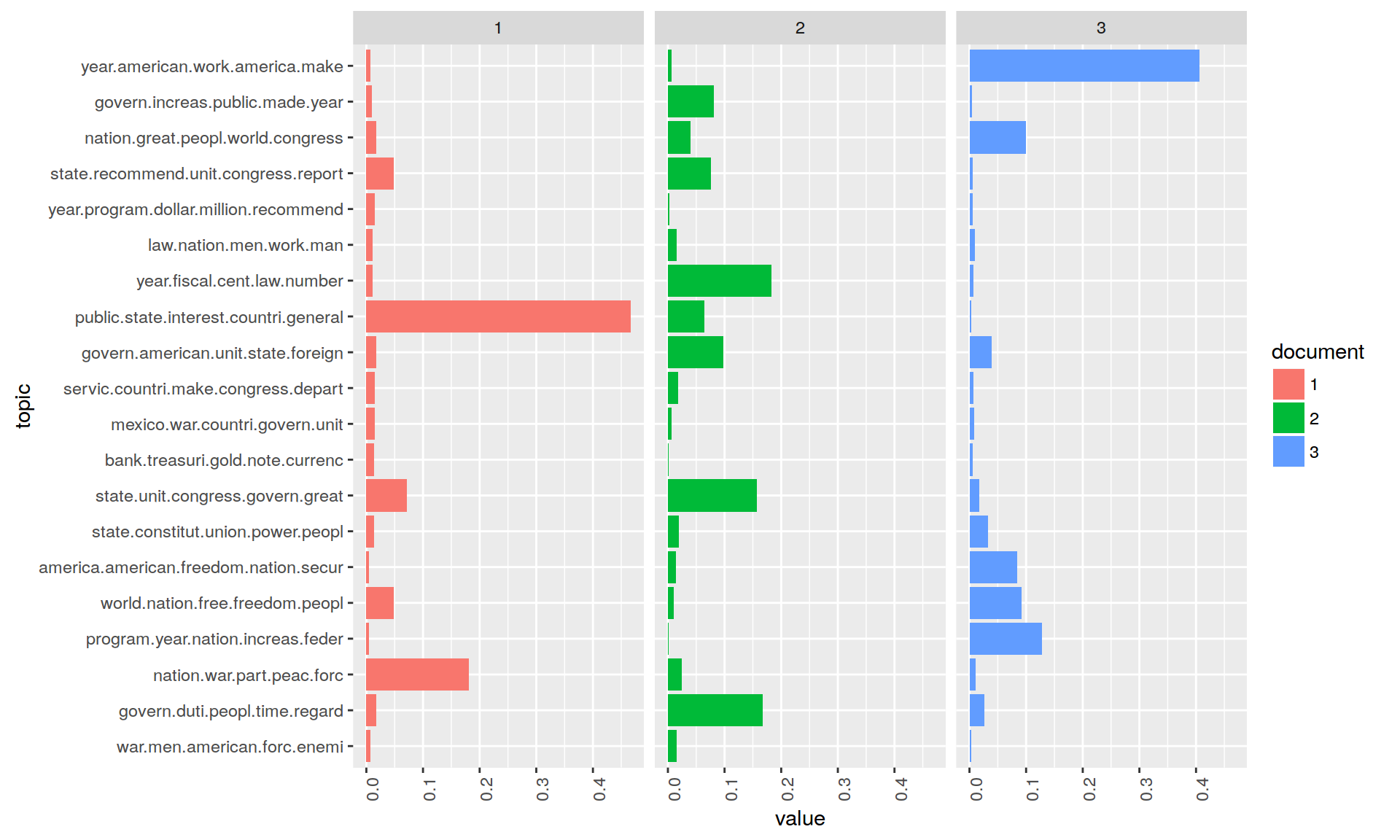

3 Topic distributions

The figure above shows how topics within a document are distributed according to the model. In the current model all three documents show at least a small percentage of each topic. However, two to three topics dominate each document.

The topic distribution within a document can be controlled with the Alpha-parameter of the model. Higher alpha priors for topics result in an even distribution of topics within a document. Low alpha priors ensure that the inference process distributes the probability mass on a few topics for each document.

In the previous model calculation the alpha-prior was automatically estimated in order to fit to the data (highest overall probability of the model). However, this automatic estimate does not necessarily correspond to the results that one would like to have as an analyst. Depending on our analysis interest, we might be interested in a more peaky/more even distribution of topics in the model.

Now let us change the alpha prior to a lower value to see how this affects the topic distributions in the model.

# see alpha from previous model
attr(topicModel, "alpha") 

## [1] 2.5

topicModel2 <- LDA(DTM, K, method="Gibbs", control=list(iter = 500, verbose = 25, alpha = 0.2))
tmResult <- posterior(topicModel2)
theta <- tmResult$topics
beta <- tmResult$terms
topicNames <- apply(terms(topicModel2, 5), 2, paste, collapse = " ")  # reset topicnames

Now visualize the topic distributions in the three documents again. What are the differences in the distribution structure?

# get topic proportions form example documents
topicProportionExamples <- theta[exampleIds,]
colnames(topicProportionExamples) <- topicNames
vizDataFrame <- melt(cbind(data.frame(topicProportionExamples), document = factor(1:N)), variable.name = "topic", id.vars = "document")  

ggplot(data = vizDataFrame, aes(topic, value, fill = document), ylab = "proportion") + 
  geom_bar(stat="identity") +
  theme(axis.text.x = element_text(angle = 90, hjust = 1)) +  
  coord_flip() +
  facet_wrap(~ document, ncol = N)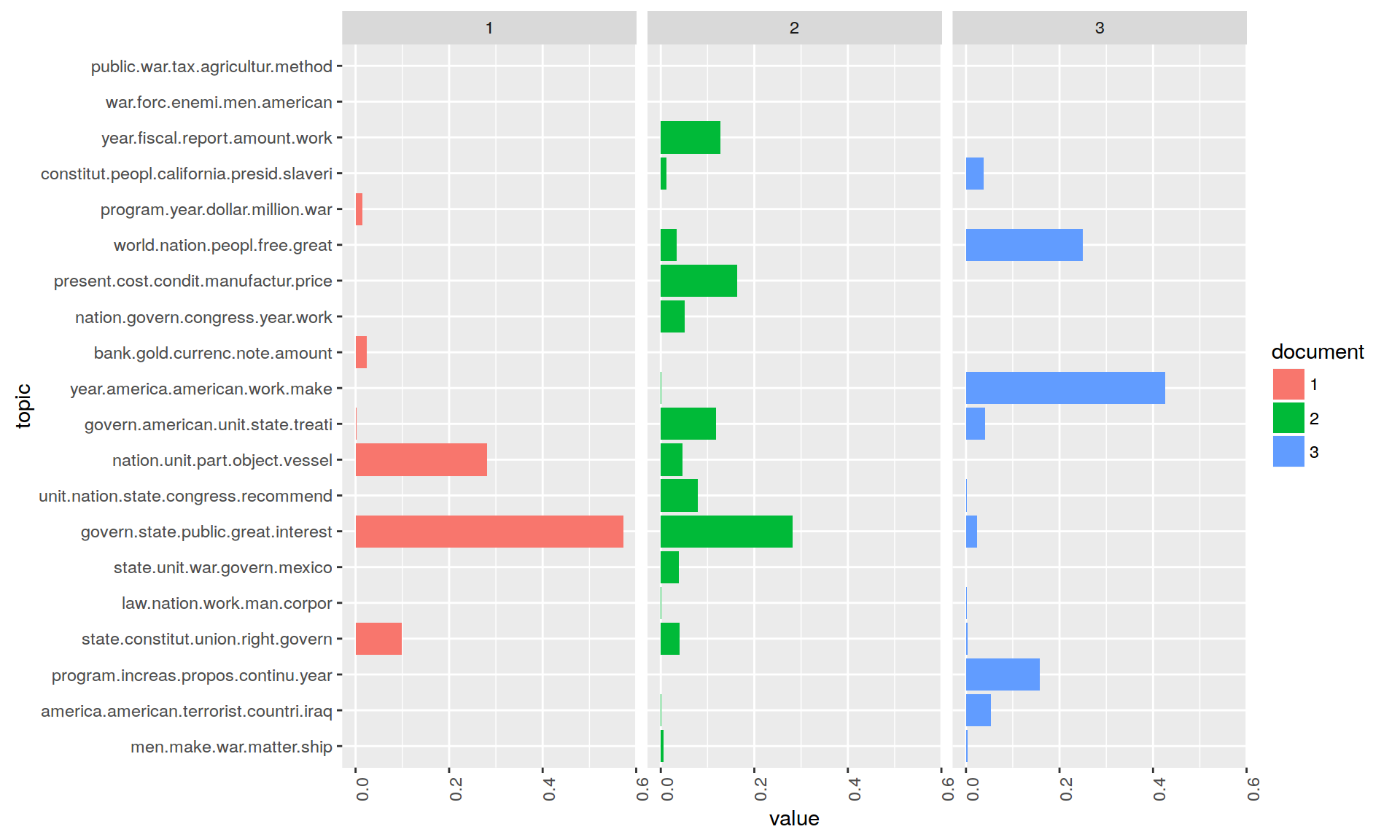

4 Topic ranking

First, we try to get a more meaningful order of top terms per topic by re-ranking them with a specific score [2]. The idea of re-ranking terms is similar to the idea of TF-IDF. The more a term appears in top levels w.r.t. its probability, the less meaningful it is to describe the topic. Hence, the scoring advanced favors terms to describe a topic.

# re-rank top topic terms for topic names
topicNames <- apply(lda::top.topic.words(beta, 5, by.score = T), 2, paste, collapse = " ")

What are the defining topics within a collection? There are different approaches to find out which can be used to bring the topics into a certain order.

Approach 1: We sort topics according to their probability within the entire collection:

# What are the most probable topics in the entire collection?
topicProportions <- colSums(theta) / nDocs(DTM)  # mean probablities over all documents
names(topicProportions) <- topicNames     # assign the topic names we created before
sort(topicProportions, decreasing = TRUE) # show summed proportions in decreased order

##  [1] "0.22522 : govern state public interest subject" 
##  [2] "0.10318 : world nation free peac peopl"         
##  [3] "0.09655 : america work job make year"           
##  [4] "0.08841 : nation govern congress system work"   
##  [5] "0.08103 : nation unit object vessel part"       
##  [6] "0.07425 : state mexico unit war amount"         
##  [7] "0.05298 : program growth feder energi propos"   
##  [8] "0.03478 : unit recommend cuba congress nation"  
##  [9] "0.02809 : govern unit american state treati"    
## [10] "0.02794 : make men matter ship peac"            
## [11] "0.02512 : terrorist america iraq terror fight"  
## [12] "0.0244 : state constitut union right principl"  
## [13] "0.02263 : program dollar fiscal million billion"
## [14] "0.02096 : manufactur present price cost tariff" 
## [15] "0.01866 : public agricultur method board cent"  
## [16] "0.01798 : year fiscal silver indian report"     
## [17] "0.01767 : war enemi forc fight victori"         
## [18] "0.01605 : law man nation corpor work"           
## [19] "0.0141 : bank gold currenc note circul"         
## [20] "0.01 : constitut california slaveri peopl slave"

We recognize some topics that are way more likely to occur in the corpus than others. These describe rather general thematic coherences. Other topics correspond more to specific contents.

Approach 2: We count how often a topic appears as a primary topic within a document. This method is also called Rank-1.

countsOfPrimaryTopics <- rep(0, K)
names(countsOfPrimaryTopics) <- topicNames
for (i in 1:nDocs(DTM)) {
  topicsPerDoc <- theta[i, ] # select topic distribution for document i
  # get first element position from ordered list
  primaryTopic <- order(topicsPerDoc, decreasing = TRUE)[1] 
  countsOfPrimaryTopics[primaryTopic] <- countsOfPrimaryTopics[primaryTopic] + 1
}
sort(countsOfPrimaryTopics, decreasing = TRUE)

##  [1] "87 : govern state public interest subject"   
##  [2] "30 : world nation free peac peopl"           
##  [3] "29 : america work job make year"             
##  [4] "20 : nation govern congress system work"     
##  [5] "13 : nation unit object vessel part"         
##  [6] "10 : govern unit american state treati"      
##  [7] "8 : terrorist america iraq terror fight"     
##  [8] "7 : law man nation corpor work"              
##  [9] "6 : make men matter ship peac"               
## [10] "6 : program growth feder energi propos"      
## [11] "3 : state mexico unit war amount"            
## [12] "3 : year fiscal silver indian report"        
## [13] "3 : war enemi forc fight victori"            
## [14] "2 : public agricultur method board cent"     
## [15] "1 : unit recommend cuba congress nation"     
## [16] "1 : bank gold currenc note circul"           
## [17] "1 : manufactur present price cost tariff"    
## [18] "1 : program dollar fiscal million billion"   
## [19] "0 : state constitut union right principl"    
## [20] "0 : constitut california slaveri peopl slave"

We see that sorting topics by the Rank-1 method places topics with rather specific thematic coherences in upper ranks of the list.

This sorting of topics can be used for further analysis steps such as the semantic interpretation of topics found in the collection, the analysis of time series of the most imprtant topics or the filtering of the original collection based on specific sub-topics.

5 Filtering documents

The fact that a topic model conveys of topic probabilities for each document makes it possible to use it for thematic filtering of a collection. AS filter we select only those documents which exceed a certain threshold of their probability value for certain topics (for example, each document which contains topic X to more than 20 percent).

In the following, we will select documents based on their topic content and display the resulting document quantity over time.

topicToFilter <- 6  # you can set this manually ...
# ... or have it selected by a term in the topic name (e.g. 'iraq')
topicToFilter <- grep('iraq', topicNames)[1] 
topicThreshold <- 0.2
selectedDocumentIndexes <- which(theta[, topicToFilter] >= topicThreshold)
filteredCorpus <- corpus[selectedDocumentIndexes]

# show length of filtered corpus
filteredCorpus

## <<VCorpus>>
## Metadata:  corpus specific: 0, document level (indexed): 0
## Content:  documents: 8

Our filtered corpus contains 8 documents related to the topic 2 to at least 20 %.

6 Topic proportions over time

In a last step, we provide a distant view on the topics in the data over time. For this, we aggregate mean topic proportions per decade of all SOTU speeches. These aggregated topic proportions can then be visualized, e.g. as a bar plot.

# append decade information for aggregation
textdata$decade <- paste0(substr(textdata$date, 0, 3), "0")
# get mean topic proportions per decade
topic_proportion_per_decade <- aggregate(theta, by = list(decade = textdata$decade), mean)
# set topic names to aggregated columns
colnames(topic_proportion_per_decade)[2:(K+1)] <- topicNames

# reshape data frame
vizDataFrame <- melt(topic_proportion_per_decade, id.vars = "decade")

# plot topic proportions per deacde as bar plot
require(pals)
ggplot(vizDataFrame, aes(x=decade, y=value, fill=variable)) + 
  geom_bar(stat = "identity") + ylab("proportion") + 
  scale_fill_manual(values = paste0(alphabet(20), "FF"), name = "decade") + 
  theme(axis.text.x = element_text(angle = 90, hjust = 1))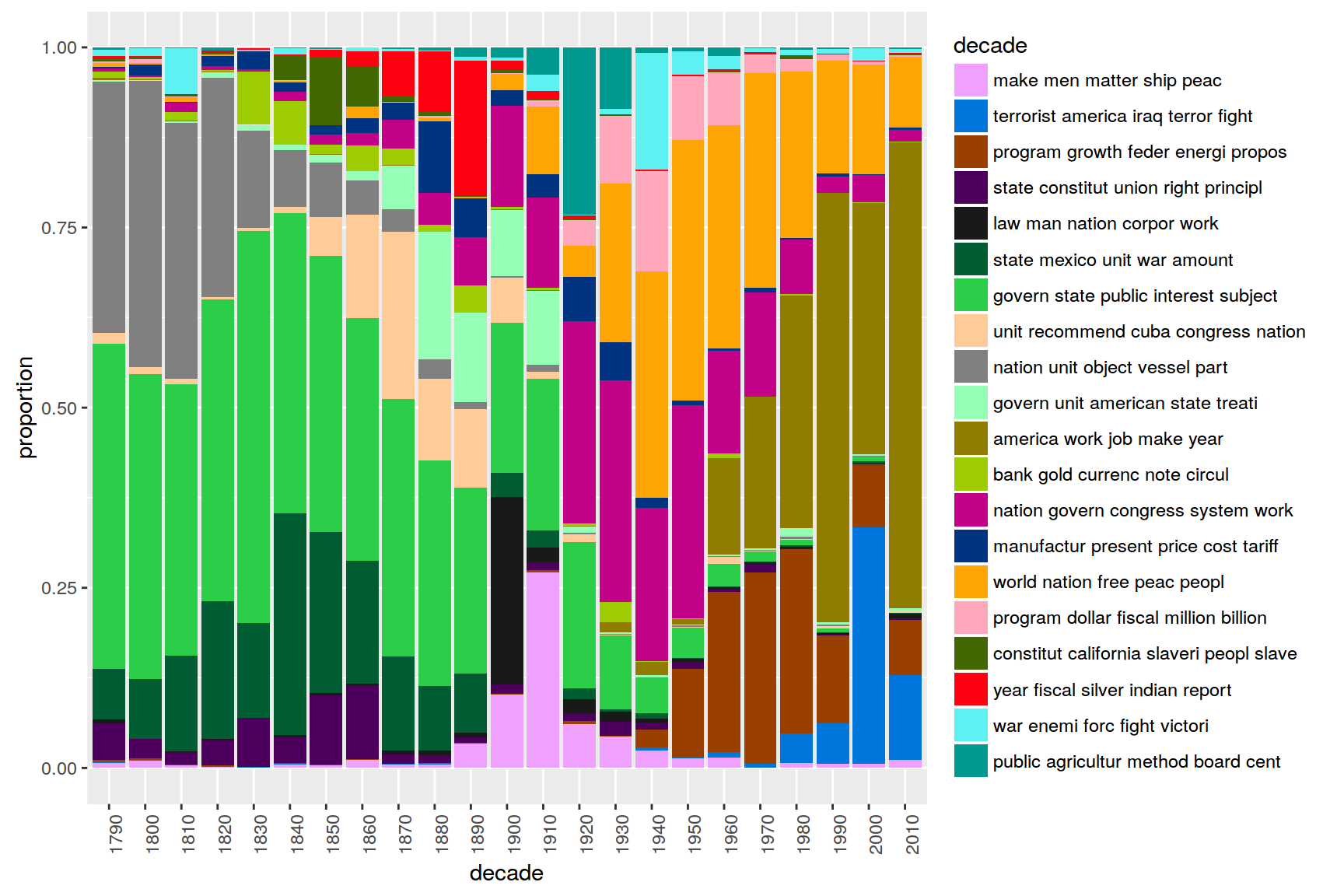

The visualization shows that topics around the relation between the federal government and the states as well as inner conflicts clearly dominate the first decades. Security issues and the economy are the most important topics of recent SOTU addresses.

7 Remark

The 231 SOTU addresses are rather long documents. Documents lengths clearly affects the results of topic modeling. For very short texts (e.g. Twitter posts) or very long texts (e.g. books), it can make sense to concatenate/split single documents to receive longer/shorter textual units for modeling.

For the SOTU speeches for instance, it may be beneficial to model on paragraphs instead of entire speeches. By manual inspection / qualitative inspection of the results you can check if this procedure yields better (interpretable) topics.

8 Optional exercises

1. Create a list of all documents that have a thematic context with economy.
2. Repeat the exercises with a different K value (e.g., K = 5, 30, 50). What do you think of the results?
3. Split the original text source into paragraphs (e.g. use strsplit(textdata$text, "\n\n")) and compute a topic model on paragraphs instead of full speeches. How does the smaller context unit affect the result?